Logical Agents
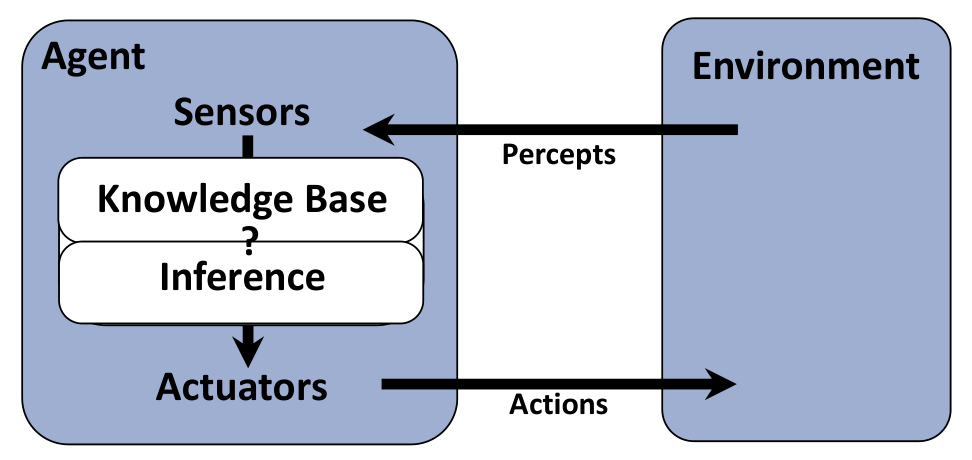
Knowledge-based agents
Knowledge Bases

在逻辑智能体中,知识库就是一系列的形式语言,我们告诉智能体可以怎么做,然后智能体就能依照我们提供的指示,从知识库中推导出新的知识。
Logical Agents
和CSP相比,逻辑智能体存放的内容更加复杂,形式更加丰富(命题逻辑、谓词逻辑)。
比如告诉一个逻辑智能体以下信息:
- 事实(facts):
- 草是绿的
- 天是蓝的
- 规则(rule):
- 吃太多糖果会生病
- 生病了就不用去学校
- 观测条件(percepts and actions):
- pat今天吃了很多糖果
智能体会推出结论:pat今天不用去学校

Wumpus world

想要让逻辑智能体解决这个问题,我们首先要将问题形式化。
Logic in general - models and entailment
- 逻辑语句(logics)就是包含了能够推出结论的信息的形式化语句(formal language)。
- 语法(syntax)定义了一个句子(sentence)应当是怎样的
- 语义(semantics)定义了句子的是真还是假(meaning)
Entailment
逻辑蕴含(entailment)指的是一者能够推出另一者
这里是知识库KB蕴含 ,即假如KB为真,那么 一定为真。逻辑蕴含关系能够让智能体得到新知识。
Models
我们说 是关于句子 的一个模型,也就是说在 的条件下 为真。我们用 表示 所有模型的集合。因此 等价于

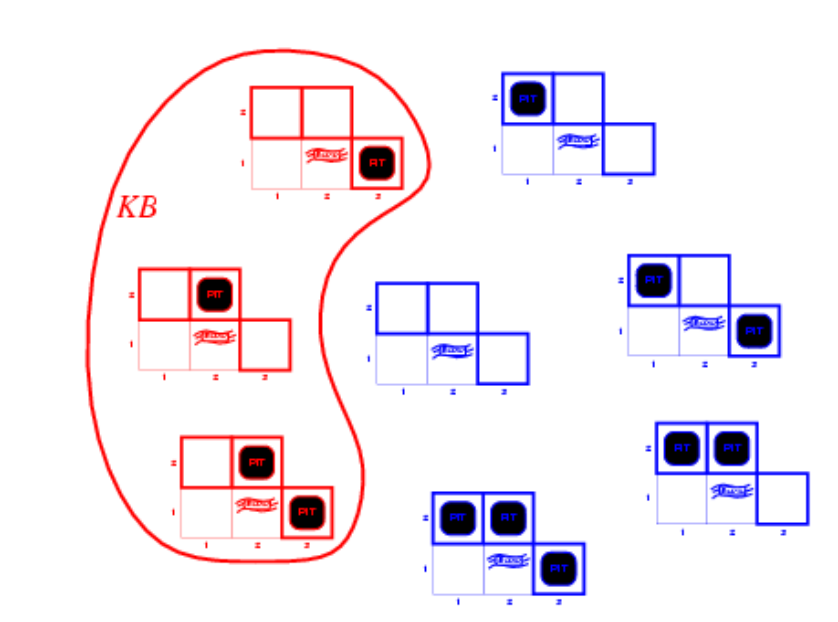
下面演示通过模型检验的方式进行逻辑推导,以前面的Wumpus world游戏为例。假如玩家已经探索了(1, 1)和(2, 1)坐标,然后可以列出所有可能的模型,再根据KB中的规则得到
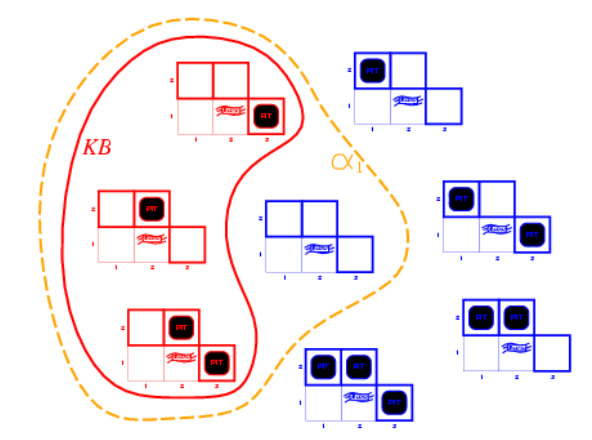
然后记语句 为“[1, 2]是安全的”,可以得到 如下:
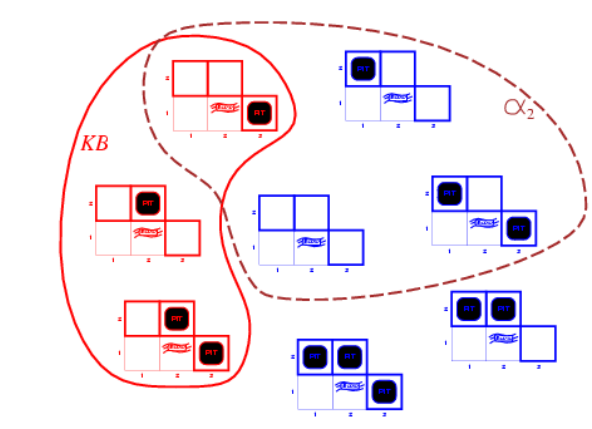
可以看出 ,所以 为真。但是如果记 为“[2, 2]是安全的”,那么得到 如下:
可以看出无法得到 为真。
Wumpus world sentence
假如想要使用推导的话,需要将这个游戏形式化。
- 令 为真表示 点上有陷阱
- 令 为真表示 点有微风
假如此时玩家探索了 坐标和 坐标,那么可以得到知识:。根据规则:“陷阱的周围有微风”,可以得到
Inference rules and theorem proving
resolution
归结法的推导:
对于两个CNF ,假如存在 和 互补,那么就归结出
也就是说想要使用归结法,要首先将逻辑表达式变成合取范式。
Resolution algorithm
使用归结法实际上是在使用反证法。假如我们希望证明 ,那么需要证明 是不可满足的。
于是我们将 给出的条件转化为合取范式(CNF),同时将 也一起放入,假如经过归结,发现得到空集,这就说明 不可满足,。
Horn Form
霍恩子句是一种更加严格的子句。在前面我们提到需要将 化为合取范式,而假如其中的子句满足至多有一个变量为正(positive),那么该子句就是霍恩子句。比如:。
使用霍恩子句是为了让子句更方便地变成肯定前件式,便于推导,比如
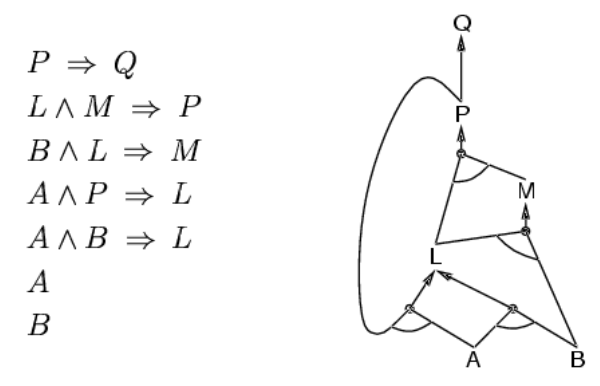
forward chaining
就是利用肯定前件式直接往后推,比如这个例子,就是在知道A,B的前提下,一步一步推导出其他条件
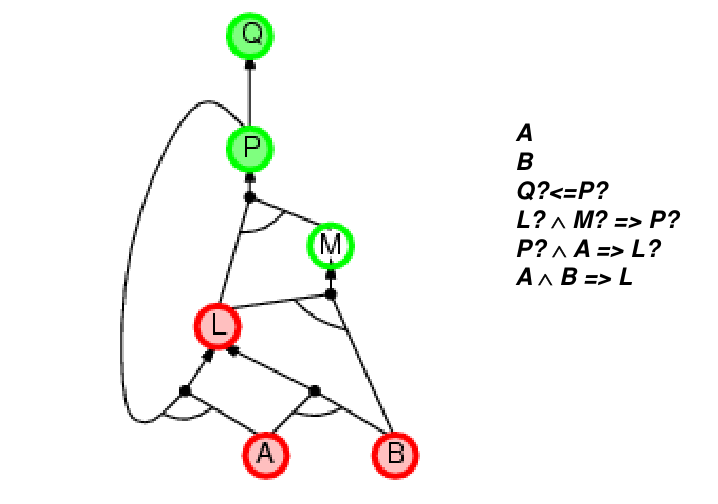
backward chaining
将forward的顺序反过来,思路为:我们需要一个条件,然后看实现这个条件还需要什么其他条件,以此类推往前追溯。
上面就是一个backwards chaining的例子。