Local Descriptor

在之前的课程中提到，每个图片都可以使用 SIFT 找到若干 key point，每个 key point 都有一个 local descriptor (feature)，表示邻域的特征。这里需要考虑如何把多个 local feature 聚合称为整张图片的 feature。

Local descriptor 的形式也较为多样。在下图中，一张图片可以识别出很多 object proposal，即一个个可能包含有物体的框。每一个 object proposal 的 feature 都可以作为一个 local descriptor。

或者一个视频可能会有很多轨迹 (trajectories)，即一个点从一个位置移动到另一个位置经过的路线。对于图片的一帧，可以找到很多关键点，那么我们通过追踪这些关键点，就能得到很多 trajectory。每个 trajectory 可以提取一个特征 (对一个点时间邻域内的像素做信息提取)。

Feature Encoding

Feature Encoding Step

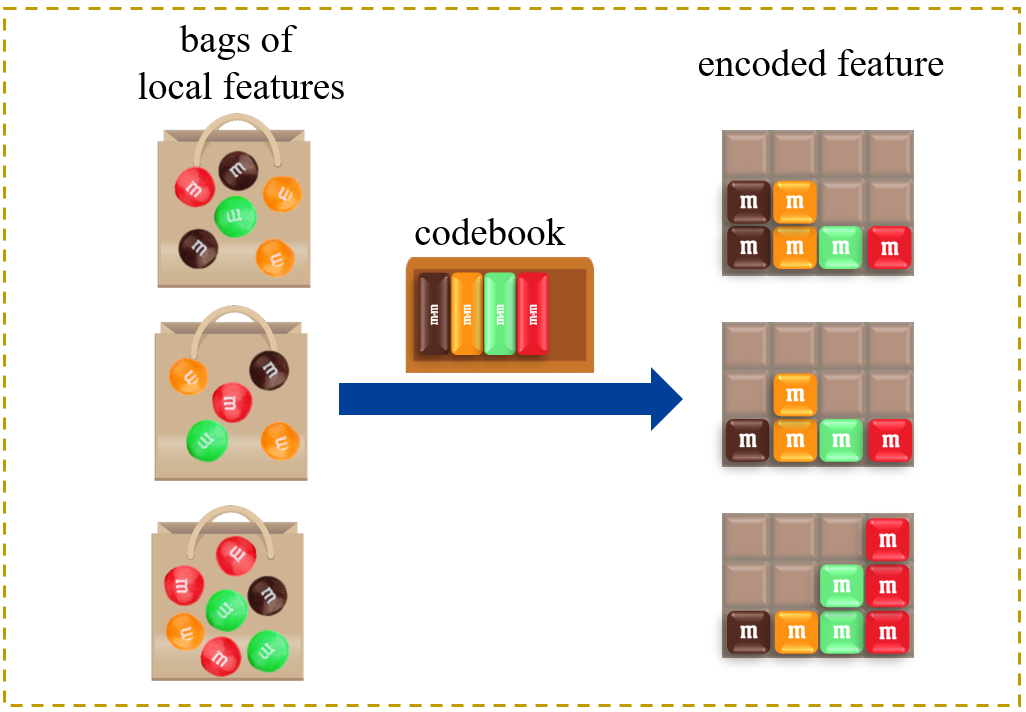
需要使用一个 codebook，将一堆 local feature 整合成一个 feature vector。步骤为：

  • 学习得到一个 codebook

    • 直观的理解，codebook 其实就是一些有代表性的 local feature
    • 比如使用 k-means 聚类，就能得到很多 cluster center，每个 cluster center 就可以作为 codebook 中的一个 word

  • 基于学到的 codebook 将局部特征进行编码

    • 下图展现最简单的方法：统计一个 bag 的某一种 local feature 出现了多少次

Example

比如说有一堆杯子，我们提取 object proposals，然后每个 proposal 得到一个 feature，最后学习到一个 codebook。在本例子中，可以认为是通过聚类得到了三个 cluster center，分别是被子的杯身、杯底和把手这三个有代表性的特征。

然后使用 codebook 对每张杯子图片的 local feature 进行 encoding。

Feature Encoding Methods

  • Encode 0-order information
    • e.g, bag-of-word (BOW)
  • Encode 1-order information
    • e.g., Vector of Locally Aggregated Descriptors (VLAD)
  • Encode 2-order information
    • e.g., Fisher vector

以上分别是编码零阶、一阶、二阶信息的方法。信息越高价，方式越复杂，但是效果也越好。

Bag-of-word (BOW)

以图片为例。

  • 每张图片得到一些 local descriptor
  • 然后将所有图片的 local descriptor 放到一起，做 cluster，cluster center 的数量即为 codebook 中 word 的数量。在下图中，共有 c1,c2,c3,c4\mathbf{c}_1,\mathbf{c}_2,\mathbf{c}_3,\mathbf{c}_4 这四个 word。
  • 最后是统计 word 在图片的 local descriptor 中的频率。

形式化地，有

Xi={xi,1,xi,2,…,xi,Ni}→C={c1,c2,…,cK}hi=[hi,1;hi,2;…;hi,K]\begin{aligned} \mathcal{X}_i=\{\mathbf{x}_{i,1},\mathbf{x}_{i,2},\ldots,\mathbf{x}_{i,N_i}\}&\xrightarrow{\mathcal{C}=\{\mathbf{c}_1,\mathbf{c}_2,\ldots,\mathbf{c}_K\}}&\mathbf{h}_i=[h_{i,1};h_{i,2};\ldots;h_{i,K}] \end{aligned}

Xi\mathcal{X}_i 代表了第 ii 张图片，xi,1\mathbf{x}_{i,1} 代表了第 ii 张图片的第 11 个 local descriptor，c1\mathbf{c}_1 为 codebook 的第一个 word，hi,1h_{i,1} 为第 ii 张图片第一个 word 的频率。

Vector of Locally Aggregated Descriptors (VLAD)

该方法得到 codebook 的方式和 BOW 相同，但是在 feature encoding 的部分还编码了一阶信息

  • 每张图片得到一些 local descriptor
  • 然后将所有图片的 local descriptor 放到一起，做 cluster，cluster center 的数量即为 codebook 中 word 的数量。在下图中，共有 c1,c2,c3,c4\mathbf{c}_1,\mathbf{c}_2,\mathbf{c}_3,\mathbf{c}_4 这四个 word。
  • 对于某个 local descriptor xi,j\mathbf{x}_{i,j}，将其归类到第 kk 个 word 中，用 c(xi,j)=kc(\mathbf{x}_{i,j})=k 表示
  • 归类完成后，将 xi,j\mathbf{x}_{i,j} 与 ck\mathbf{c}_{k} 做差。从而第 kk 个单词可以得到

vi,k=∑j=1Niδ(c(xi,j)=k)(xi,j−ck)\mathbf{v}_{i,k} = \sum_{j=1}^{N_i} \delta(c(\mathbf{x}_{i,j})=k)(\mathbf{x}_{i,j}-c_{k})

  • 最后得到 vi=[vi,1;vi,2;⋯ ;vi,K]\mathbf{v}_i=[\mathbf{v}_{i,1}; \mathbf{v}_{i,2};\cdots; \mathbf{v}_{i,K}]，即为总的特征向量。

VLAD 是一种比较实用的方法，效果比 BOW 好，同时又不会比 Fisher vector 差太多。

Fisher Vector

引入二阶信息(标准差，方差等)

首先引入高斯混合模型 (GMM)：
θ={π1,μ1,σ1;…;πK,μK,σK}\boldsymbol{\theta}=\{\pi_1,\boldsymbol{\mu}_1,\boldsymbol{\sigma}_1;\ldots;\pi_K,\boldsymbol{\mu}_K,\boldsymbol{\sigma}_K\} 为 GMM 的参数。然后可以得到

p(x1,x2,…,xN∣θ)=∏i=1Np(xi∣θ)p(x_1,x_2,\ldots,x_N|\theta)=\prod_{i=1}^Np(x_i|\boldsymbol{\theta})

其中

p(xi∣θ)=∑k=1Kp(xi∣θk)p(θk)=∑k=1Kp(xi∣μk,σk)πkp(x_{i}|\boldsymbol{\theta}) =\sum_{k=1}^{K}p(x_{i}|\theta_{k})p(\theta_{k}) =\sum_{k=1}^{K}p(x_{i}|\mu_{k},\sigma_{k})\pi_{k}

Fisher vector 的形式化描述为：

FθXi=1Ni∑j=1Ni∇θlog⁡p(xi,j;θ)\mathcal{F}_{\boldsymbol{\theta}}^{\mathcal{X}_i}=\frac1{N_i}\sum_{j=1}^{N_i}\nabla_{\boldsymbol{\theta}}\log p(\mathbf{x}_{i,j};\boldsymbol{\theta})

其中 xi,j\mathbf{x}_{i,j} 就是第 ii 个样本的第 jj 个 local descriptor。然后将 p()p() 函数带入，求导得到：

Fμ,kXi=1Niπk∑j=1Niγi,j(k)(xi,j−μkσk)Fσ,kXi=1Ni2πk∑j=1Niγi,j(k)[((xi,j−μk)2σk2)−1]\begin{aligned} &\mathcal{F}_{\boldsymbol{\mu},k}^{\mathcal{X}_i}=\frac{1}{N_i\sqrt{\pi_k}}\sum_{j=1}^{N_i}\gamma_{i,j}(k)(\frac{\mathbf{x}_{i,j}-\boldsymbol{\mu}_k}{\boldsymbol{\sigma}_k})\\ &\mathcal{F}_{\boldsymbol{\sigma},k}^{\mathcal{X}_i}=\frac{1}{N_i\sqrt{2\pi_k}}\sum_{j=1}^{N_i}\gamma_{i,j}(k)[(\frac{(\mathbf{x}_{i,j}-\boldsymbol{\mu}_k)^2}{\boldsymbol{\sigma}_k^2})-1] \end{aligned}

其中

γi,j(k)=πkN(xi,j;μk,σk)∑k~=1Kπk~N(xi,j;μk~,σk~)\gamma_{i,j}(k)=\frac{\pi_k\mathcal{N}(\mathbf{x}_{i,j};\boldsymbol{\mu}_k,\boldsymbol{\sigma}_k)}{\sum_{\tilde{k}=1}^K\pi_{\tilde{k}}\mathcal{N}(\mathbf{x}_{i,j};\boldsymbol{\mu}_{\tilde{k}},\boldsymbol{\sigma}_{\tilde{k}})}

最后得到 2Kd2Kd 维 (dd 为 local descriptor 的维度) 的 Fihser vector：

[Fμ,1,Fσ,1;Fμ,2,Fσ,2;…;Fμ,K,Fσ,K][\mathcal{F}_{\boldsymbol{\mu},1},\mathcal{F}_{\boldsymbol{\sigma},1};\mathcal{F}_{\boldsymbol{\mu},2},\mathcal{F}_{\boldsymbol{\sigma},2};\ldots;\mathcal{F}_{\boldsymbol{\mu},K},\mathcal{F}_{\boldsymbol{\sigma},K}]

式中 Fμ,i\mathcal{F}_{\boldsymbol{\mu},i} 为一阶信息，Fσ,i\mathcal{F}_{\boldsymbol{\sigma},i} 为二阶信息。