Zero-shot and Few-shot Learning
Zero-shot Learning
主要解决训练集和测试集在种类上的差异。在之前的机器学中,训练集和测试集的种类总是相同的;而在这里,则需要考虑训练集、测试集种类不完全一样的问题。
Training/testing categories
记
- Training categories:
- Testing categories:
传统机器学习中,
在这里,需要考虑 ,即
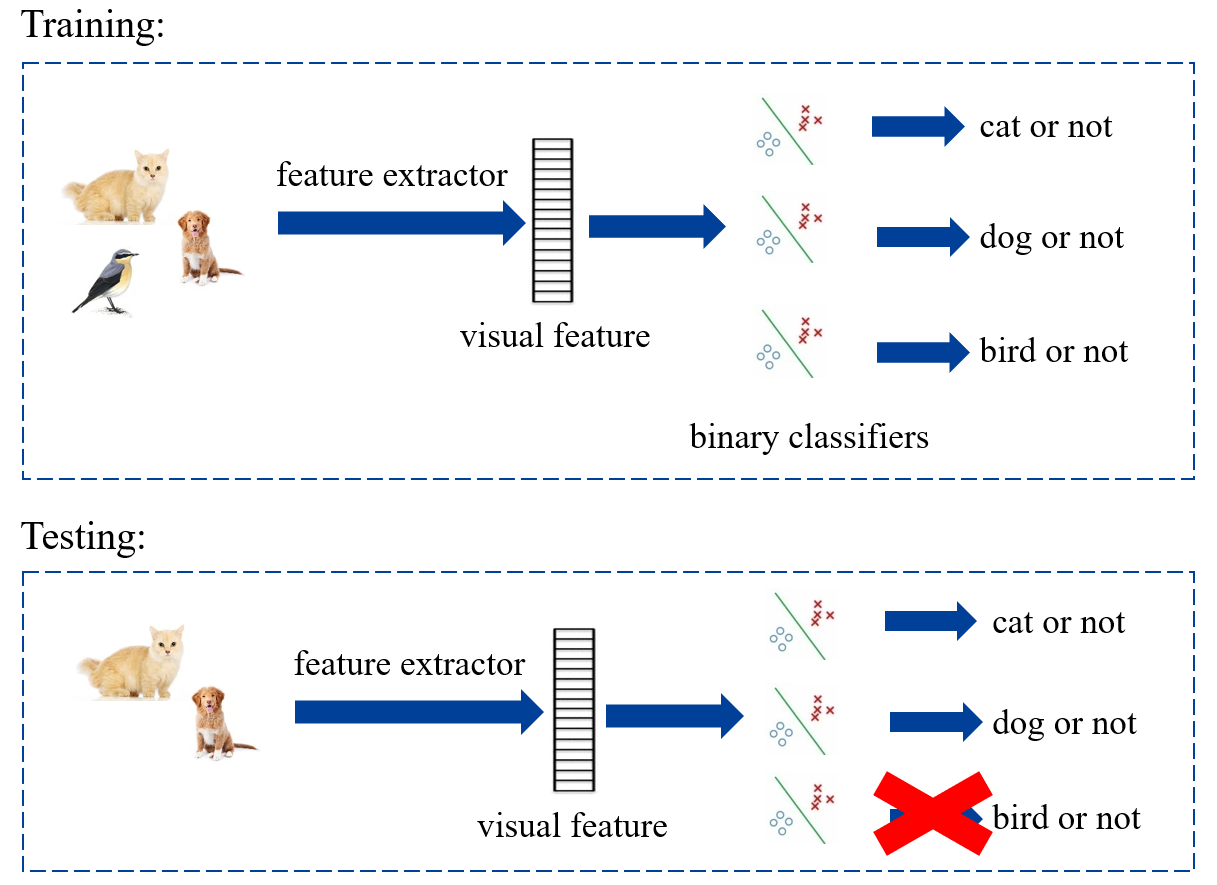
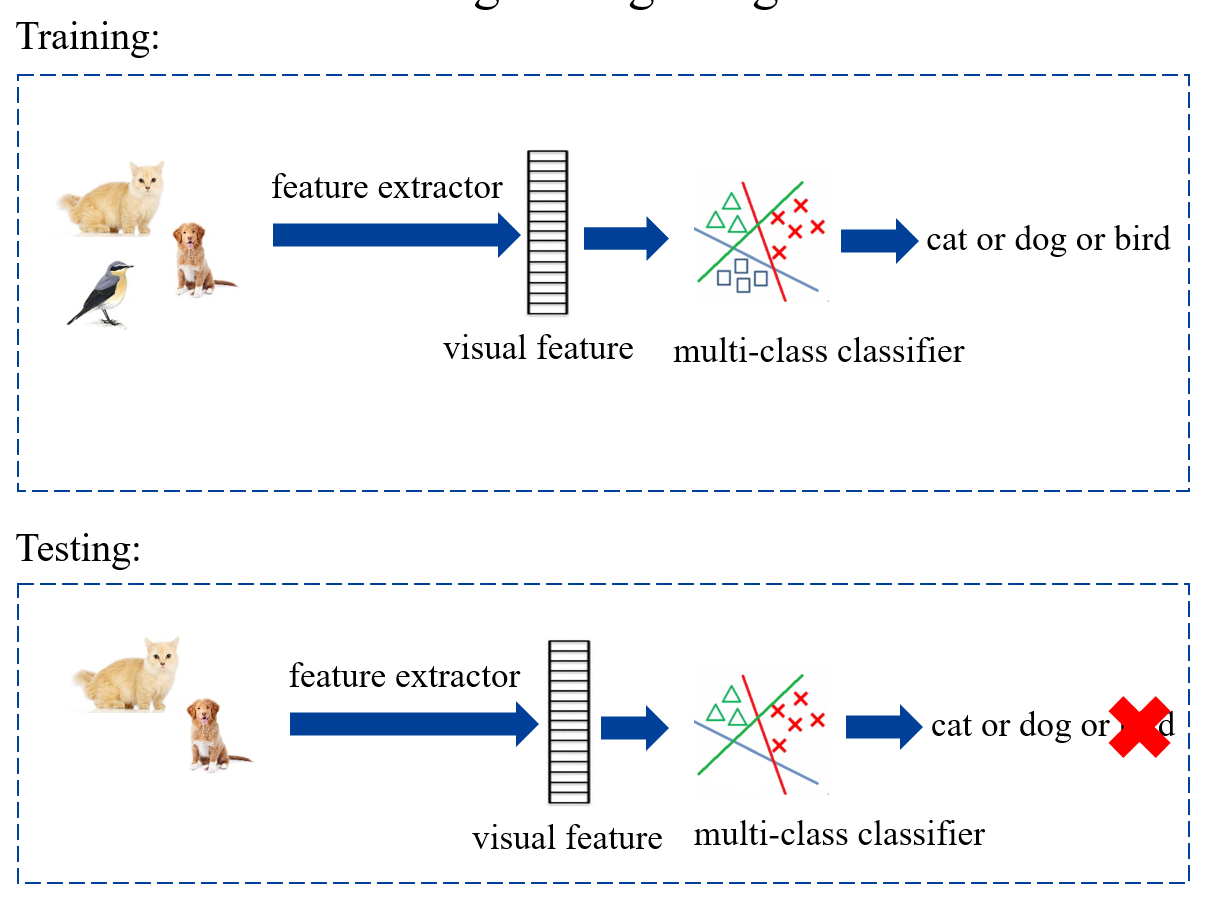
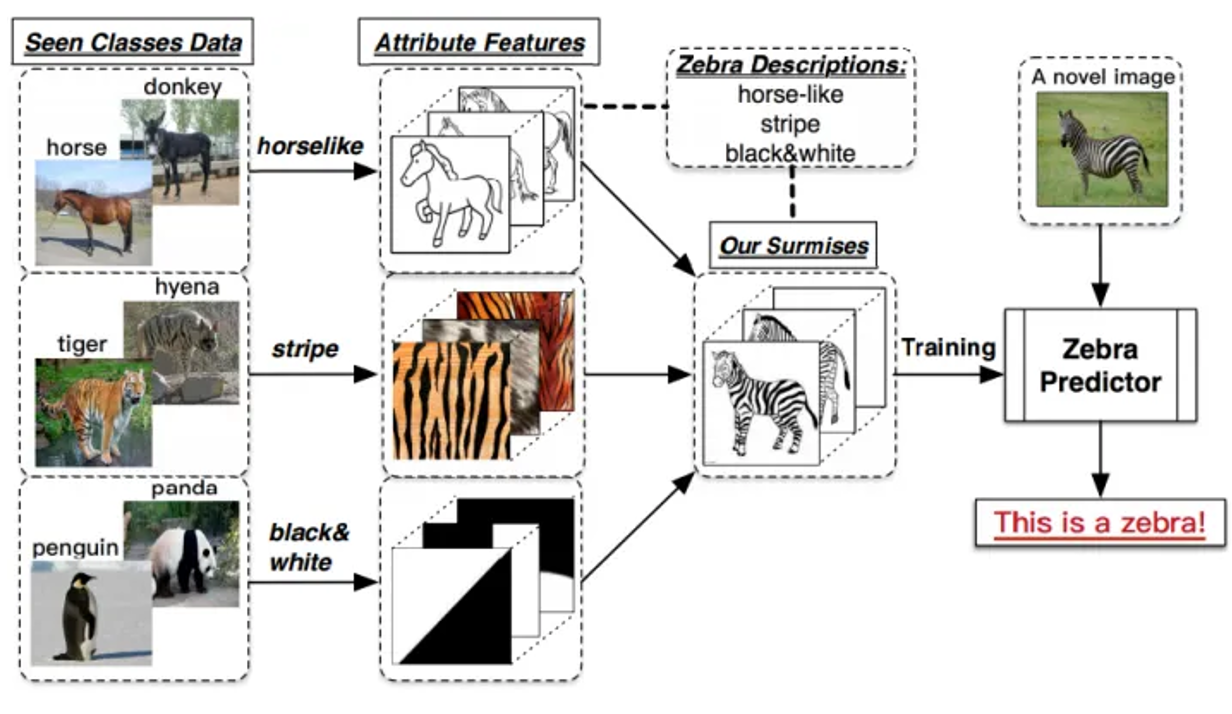
例如在下图展现的例子中,测试集就出现了训练集没有的斑马
首先考虑测试集中同样被训练集包含的部分,即:。此时处理较为简单,如果是训练多个二分类器,那么测试集中不存在的类对应的二分类器直接不使用:
如果是训练一个多分类器,那么舍弃测试集中不存在的类别:
但是如果需要考虑训练集中不存在的部分,即:,则需要使用 Zero-shot Learning 方法。
Zero-shot Learning
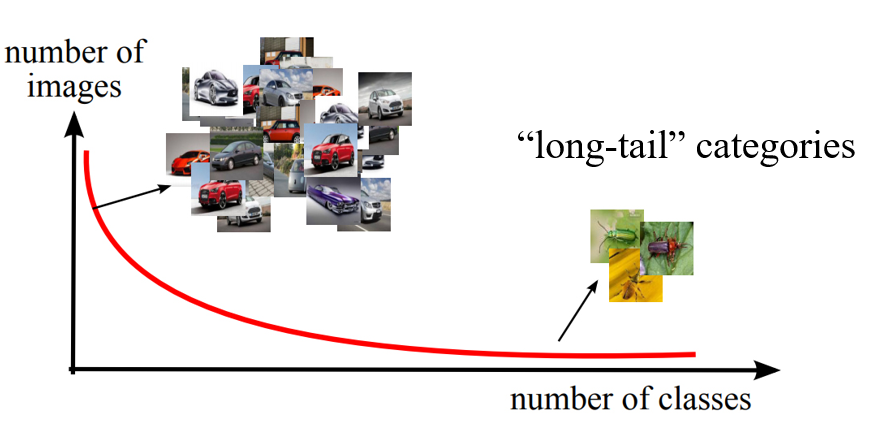
Zero-shot Learning 的现实意义是,从网络上收集数据时,根据长尾效应,有些数据非常多,但有些数据会很少甚至没有;或者说有些事物是新出现的,因此已有的数据很少。
zero-shot learning 的核心是知识迁移。同时在 zero-shot learning 中,训练集的样本种类称为 seen categories,测试集中的种类称为 unseen categories。
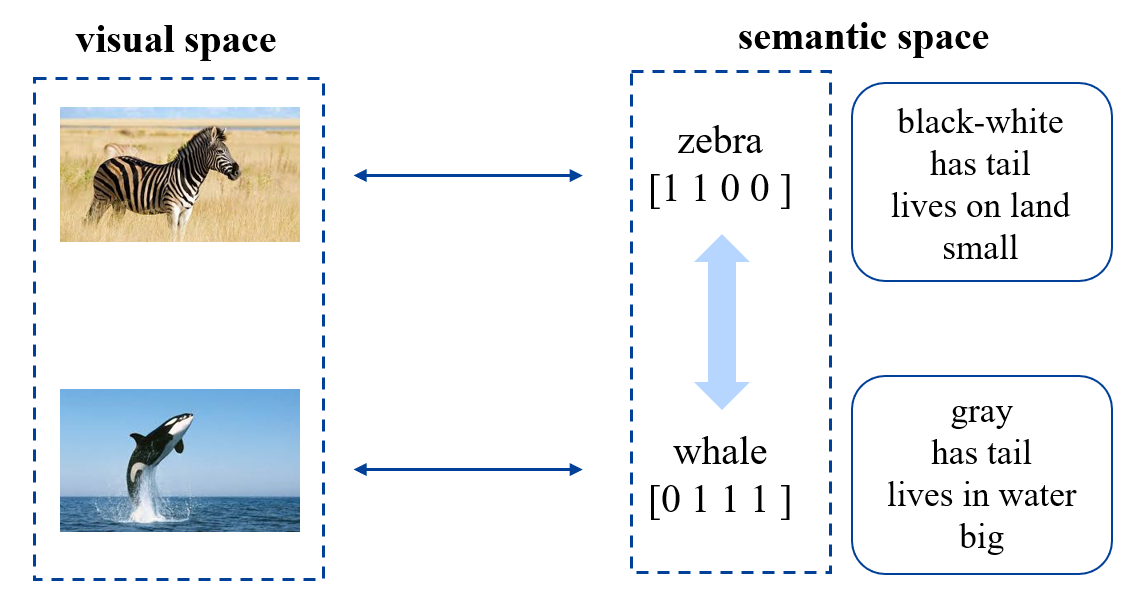
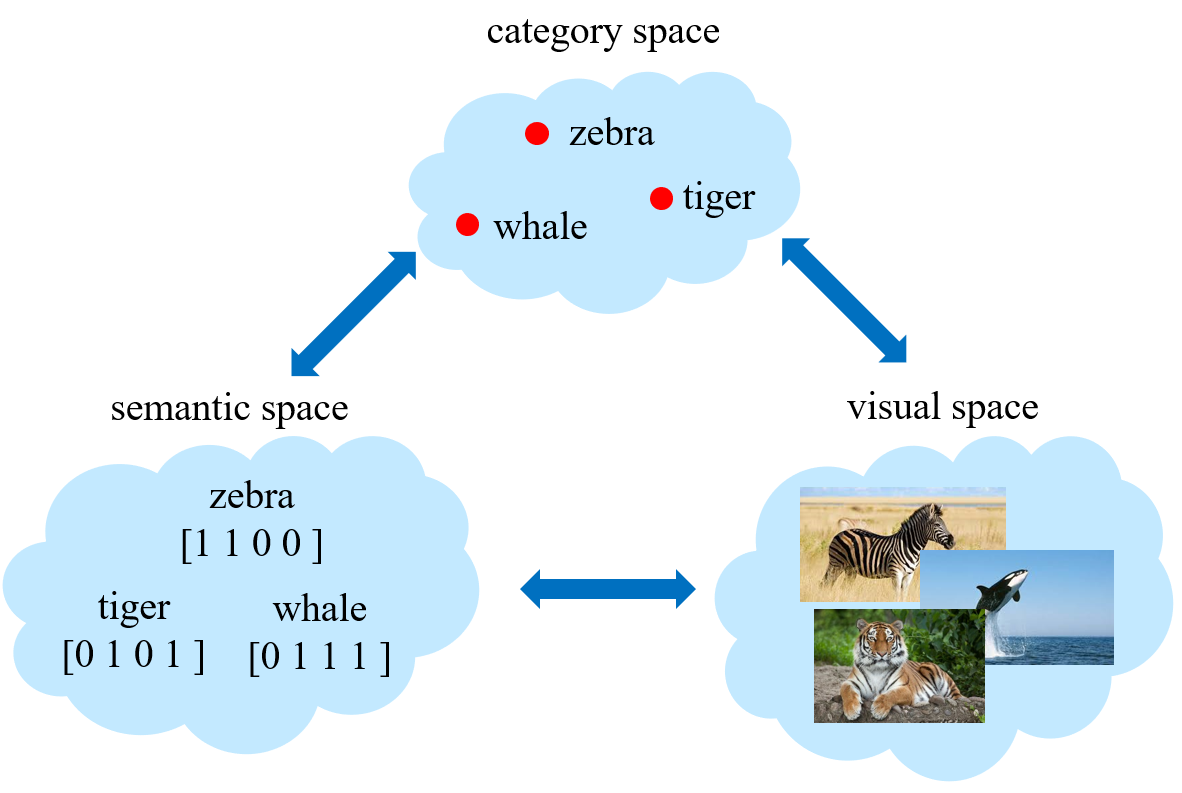
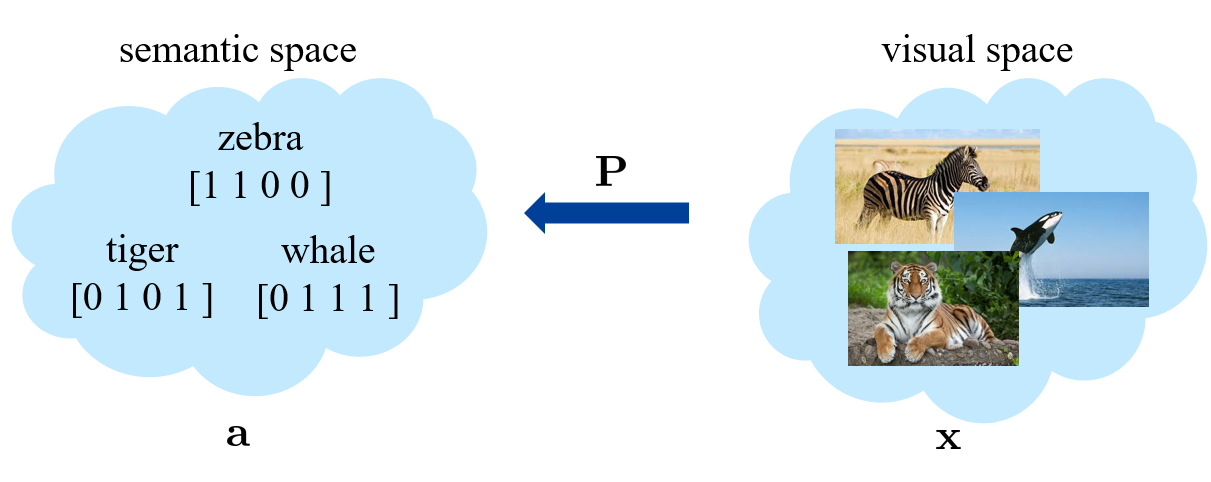
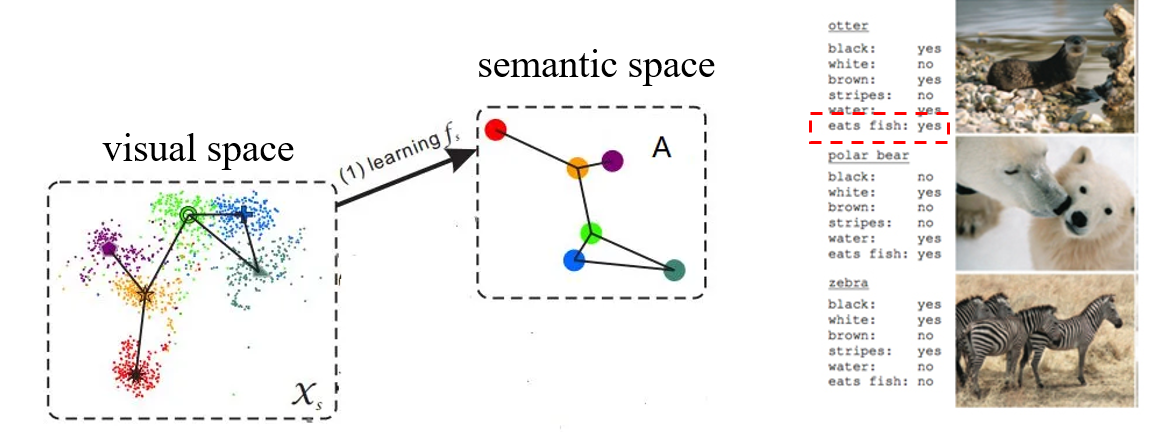
seen categories 和 unseen categories 之间利用 category-level 的语义信息(semantic information)进行连接,语义信息包括属性(attributes)或者描述(category descriptions)。对于一张图片,我们会将其从视觉空间(visual space)映射到语义空间(semantic space)。
manually annotated attribute vector
首先考虑将 attribute vector 作为语义信息。比如下方右图中,每行为一个 category,每列则为一个 attribute。那么每个 category 都有一个 attribute vector。
- 优点:准确,信息丰富。
- 缺点:标注的成本非常高。对于两个相近的种类,比如两种鸟,想要区分,就需要考虑非常细节的信息。
下面展示根据 attribute vector 如何预测一个新的种类。其核心思想就是从 seen categories 里学习不同的 attributes,然后应用于 unseen categories。
free category-level information
即通过一些免费的方法
-
textual feature of wiki page: 比如说可以通过维基百科中对一个种类的文本描述,可以进行爬取并且提取文本特征,作为语义信息。
-
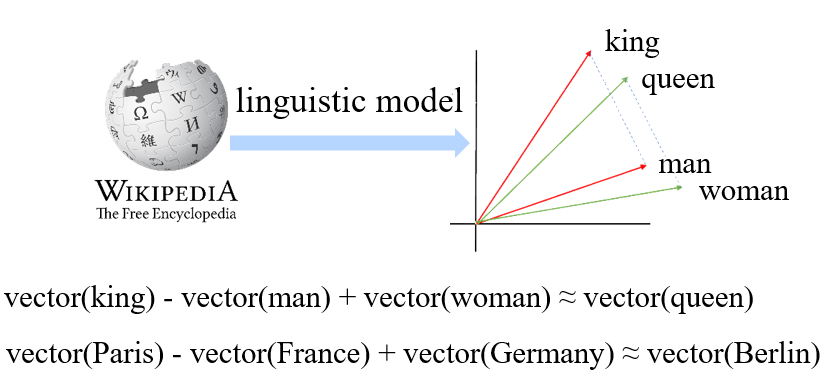
word vector of category name: 使用一个大型的语言学模型(linguistic model)进行训练,为每一个单词获得一个 word vector,这个 vector 中含有很强的语义信息,比如可以加减。
-
优点:成本低,基本免费
-
缺点:获取信息噪音大,且信息量相比 attribute vector 更少。
Zero-shot learning methods
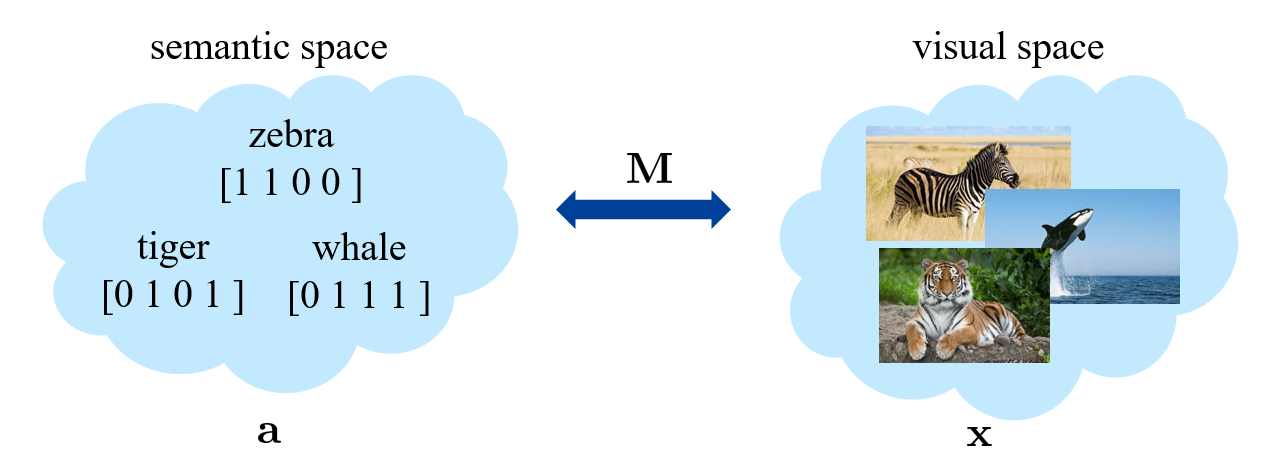
传统机器学习需要学的是从 visual space 到 category space 的映射,而 zero-shot 则需要多考虑一个 semantic space。
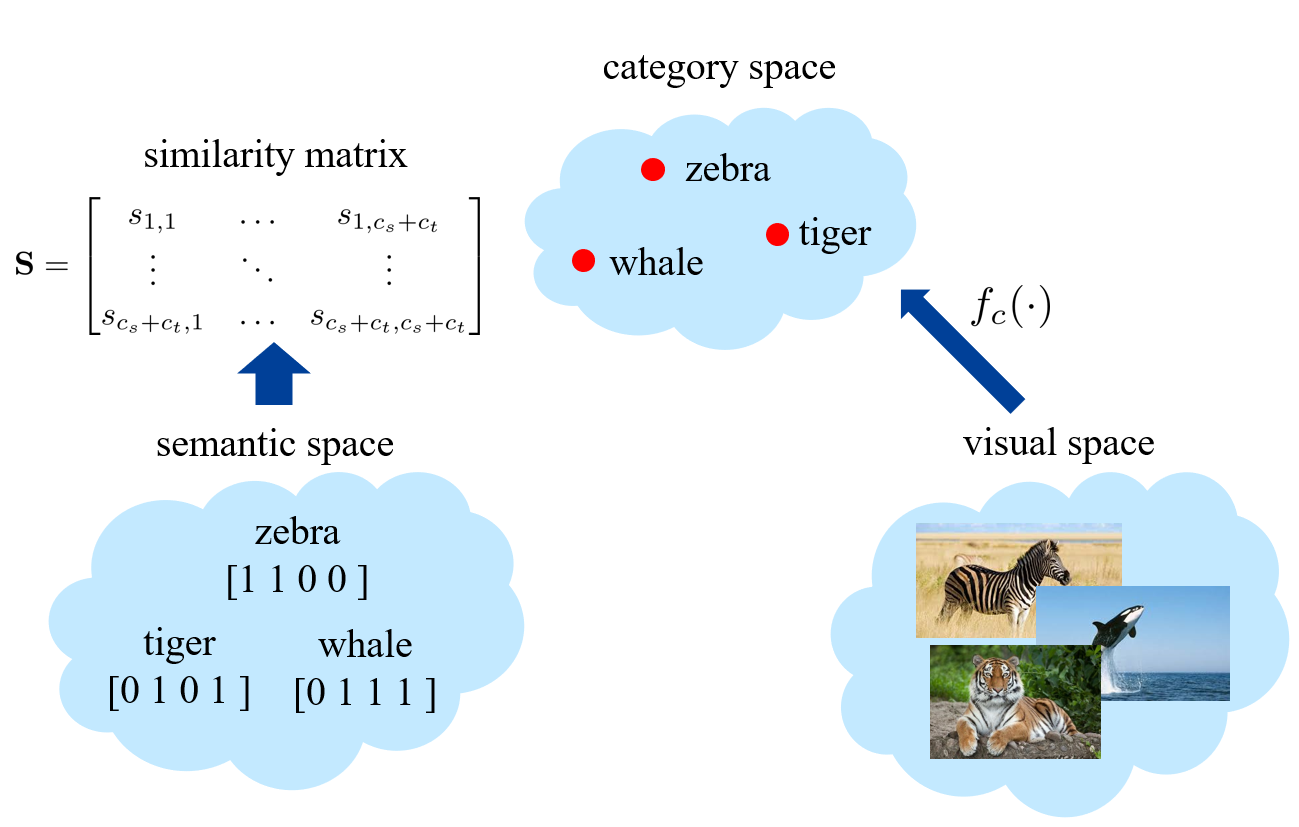
semantic relatedness methods
第一步计算所有 categories 两两之间的相似度,得到一个相似度矩阵(similarity matrix);第二步则可以进行从 visual space 到 category space 的映射。
映射的方式为:
- 首先能够训练得到 seen categories 的二分类器
- 然后将这些分类器按照相似度矩阵生成 unseen categories 的二分类器 。其中相似度矩阵的参数需要进行一些归一化操作。
这种方法较为粗糙,性能也比较差。
semantic embedding methods
方法1:学习从 visual space 到 semantic space 的映射,这里考虑的是矩阵的映射。
- 训练过程: ,其中 指的就是样本 对应的 category。
- 测试过程:
方法2:相当于是将 visual space 和 semantic space 投影到一起。
- 训练过程:,式中 称为 compatibility score。训练过程就是希望当 时,让 比 尽量小。
- 测试过程:。
方法3:和方法2类似,同样是学习一个矩阵 。记 。
- 训练过程:。这里最关键的是第一项,后面几项为约束项,不太重要。
- 测试过程:
synthetic methods
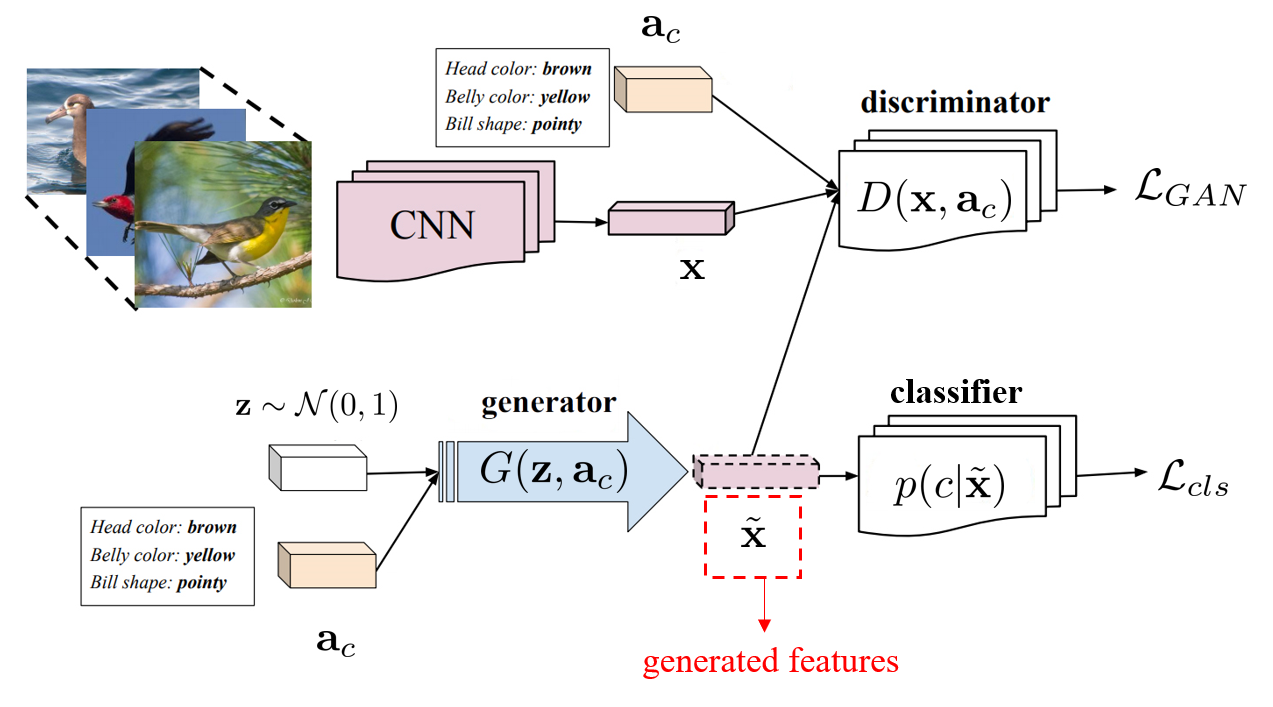
希望能够生成训练集中不存在的样本。因此需要学习从 semantic space 到 visual space 的映射 ,输出可以为图片,也可以是一个 visual feature。下面为一个示例方法:
- 左上角为图片的特征提取器,可以从真实的图片中提取 visual feature 。
- 左下角用于从 semantic vector 生成 visual feature。同时这里还使用高斯分布随机生成了 ,用于给一个 category 生成多个 visual feature 。
- 右上角为判别器 ,希望将 判别为真,将 判别为假。这里利用 GAN 的训练方法,就能是的生成的 比较真实。
- 右下角希望生成的 能够符合 category。
训练阶段使用 seen categories,在测试阶段使用 unseen categories。
Problems in Zero-shot learning
Projection domain shift
对于同一个属性,在不同的类别中,差别可能非常大。比如斑马和虎鲸都有尾巴,这两个 categories 虽然都有这一属性,但是在图片上差别非常大。
解决思路:使用无标签的数据将 visual space 到 semantic space 的映射迁移到 unseen categories 上。
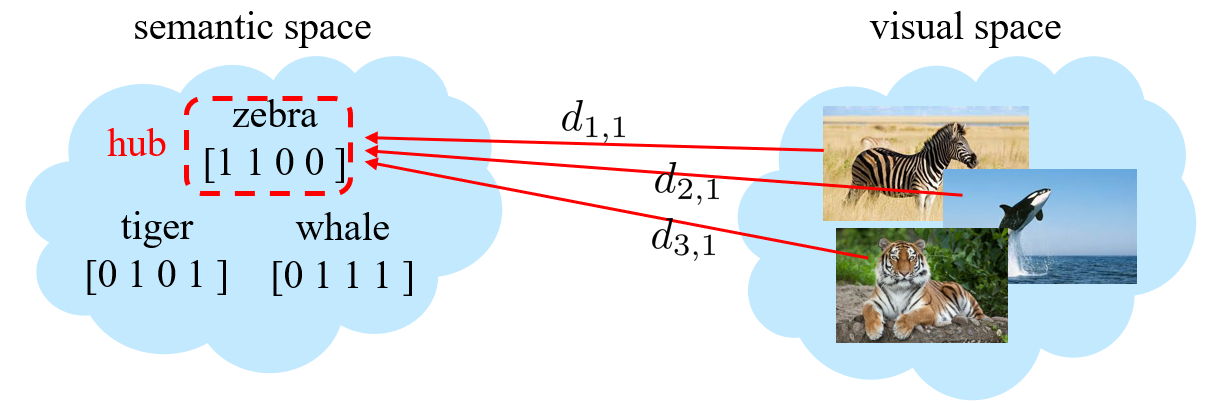
Hubness problem
比如学习到一个映射,并且将这个映射作用于测试样本,发现可能大多数的样本都被映射到同一个或少量几个 unseen categories 上。原因可能是距离度量学习的不是很合理。
解决思路:
- 对 distance 做 normalize。,。分母是对不同测试样本求和,这使得每个 category 的 distance 都得到了约束。
- 用排序代替 distance,看样本 在哪个种类 中排名最靠前。,
Semantic gap
有些属性和视觉信息不相关,此时无法学到这个属性到视觉空间的映射。比如北极熊会吃鱼,这一点就通常无法从图片中看出来。
解决方案:重新 align 一下 attribute vector。首先仍然需要学习从 visual space 到 semantic space 的映射 ,使用之后得到一系列的 categories 的 semantic vector 。对于真实的 ,则使用K近邻算法,搜索到最近的 个 ,将这 个 的平均值作为新的 。新的 离原来的比较近,但是效果更好。
Generalized zero-shot learning
对于 generalized zero-shot learning,之前的方法也都完全适用。但是在测试集上进行预测时,会出现 seen bias,也就是 seen categories 的得分会普遍高于 unseen categories。
解决方案:
- 对于 seen categories 的 score,直接减去一个常数
- hierarchical prediction。首先对于一个 test sample,先判断其为 seen 和 unseen,然后再在 seen categories 和 unseen categories 中选择。
Modern (Pseudo) zero-shot learning
改变了 zero-shot learning 的范式,让训练集不受限制。
- 训练:收集大量的图片-文本对进行训练,得到 Text Encoder 和 Image Encoder。
- 推理:对大量文本试用 Text Encoder 得到文本特征,然后与 Image Encoder 提取得到的图片特征进行匹配。

Few-shot Learning
和 zero-shot 类似,但是并非测试集中包含训练集中不存在的 categories,而是某些种类在训练集中只有少量。
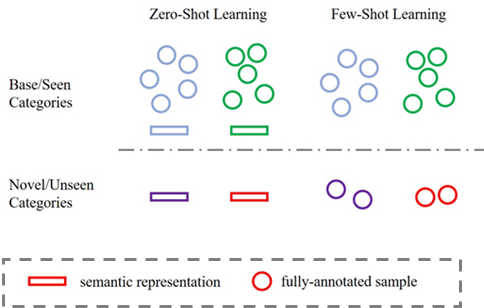
在 few-shot learning 中,不同的种类可以分为 base categories 和 novel categories ,划分依据为训练集数量。base categories 有充足的数量,而 novel categories 只有少量样本。
下图展示 zero-shot 和 few-shot 的不同。zero-shot 需要 semantic 的信息,而 few-shot 通常不用。
few-shot learning 希望提升 novel categories 的分类性能。
Meta-learning
Learn a learning strategy to adjust well to a new few-shot learning task。即学习学习的方法。
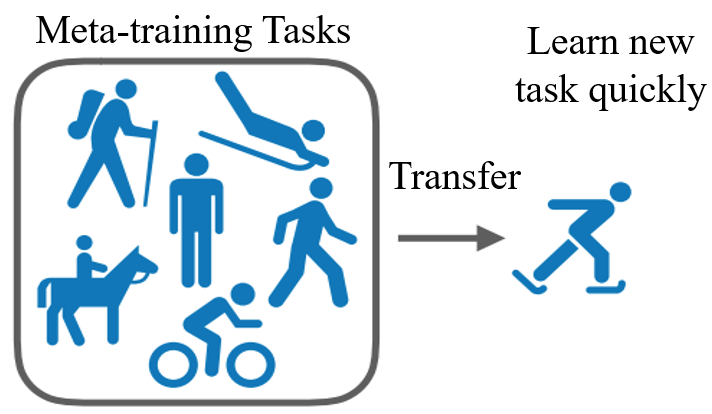
由于 meta-learning 比 learning 更高一层,所以引入 meta-training 和 meta-testing。在 meta-training 阶段,会学习很多 task;而在 meta-testing 阶段,则会有新的 task,希望将原来学习的经验迁移到新的 task 上。比如之前学过滑雪,那么在学习滑冰这个新的任务时,应该能学的更快。
- 在 meta-learning 阶段
- 从 meta-training set 中提取 training/support set 作为训练数据,数据为 N-way K-shot,也就是有 个 categories,每个 category 分别有 个 training samples。
- 从 meta-training set 中提取 test/query set 作为测试数据。
- 上述两步合称为一个 task。总共需要构建很多个 task。
- 在这个阶段可以学到很多先验知识。
- 在 meta-testing 阶段,同样选择 N-way K-shot 的 training set,以及选择 test/query set。

MAML
一个具体的 meta-learnin 的方法。
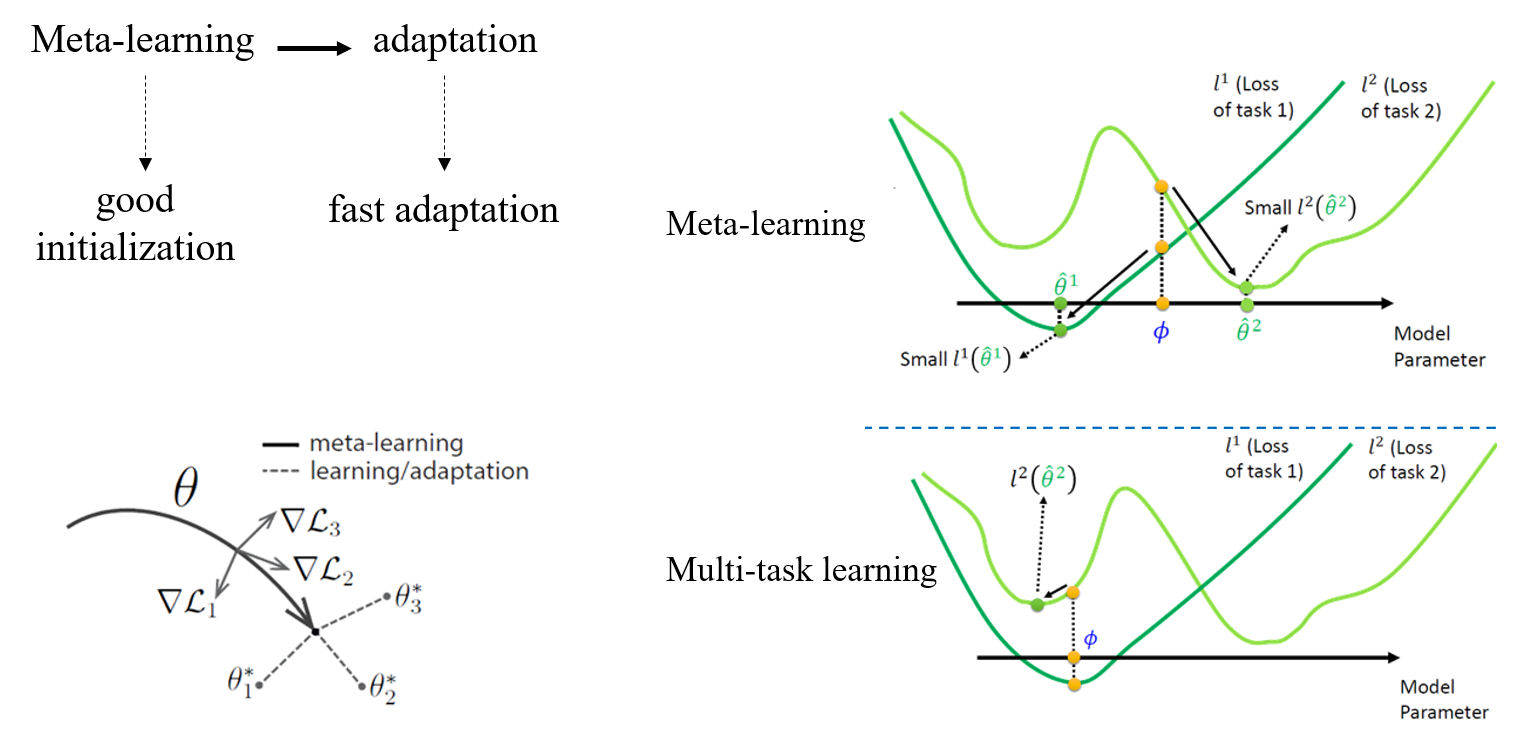
MAML 的目标是,优化模型初始化参数,使得在新的 task 中,只需要很少几步就能完成训练。即 fast adaptation to a new task。
- 假设模型参数为 ,想要将其迁移到一个新的 task 上,那么将其更新为
- meta-learning 的目标为:
- 因此对 进行优化
下图展示了 MAML 在模型初始化参数优化方面的作用,图中蓝色的 表示的就是通过 MAML 选取的初始化参数,该参数在不同的任务中(两条不同的绿色曲线)更容易达到最小值点,而不是像 Multi-task Learning 那样只能达到极小值点。
Metric learning
Learn a semantic embedding space using a distance loss function。总体思路是计算 query sample 和 support set 中每个 sample 的相似度,通过比较相似度来预测标签。
Relation Network

提取所有图片的 feature,然后通过 relation model 判断两个 feature 是否为同一个种类。
Prototypical Network
- 首先学习一个从样本到 feature 的 mapping function
- 为每个 class 生成 prototype。这里的 prototype 相当于 K-means 算法中的 centroid,就是用于代表一个类。最简单的生成方法就是取平均。
- 对于测试数据,则试用 softmax 选取最近的 class。
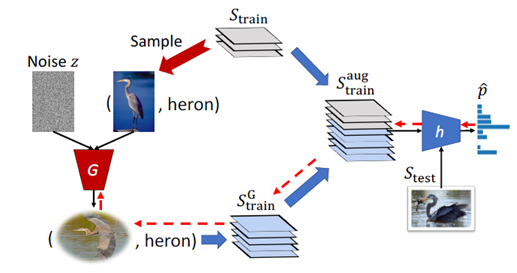
Synthetic method
Synthesize more data from the novel classes to facilitate the regular learning。和 zero-shot learning 中生成数据相似,只是这里是从少量的样本生成大量的样本。
总体流程包含两块:
- 从 base class 得到生成模型(synthesizer model)。
- 使用生成模型,基于少量的 novel class 的样本,生成大量同类样本。
方法1:左侧是生成器,右侧是分类器,两者共同训练。
方法2:
- 首先使用 encoder 捕捉同种类差异(intra-class difference)
- 然后捕捉到的差异迁移到新的种类上