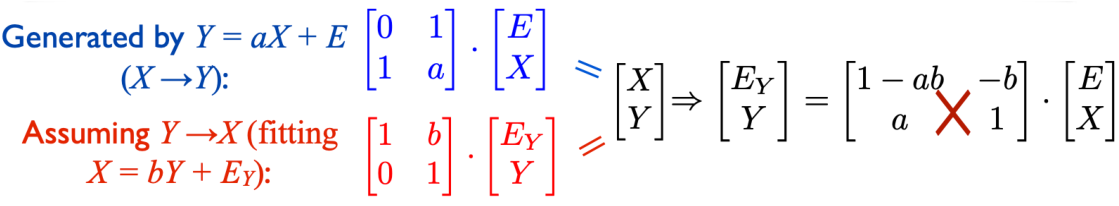Causal inference and causal discovery
Association vs. Causation (Intervention)
What Is Association?
- An associational concept is any relationship that can be defined in terms of a joint distribution of observed variables
- The term “association” refers broadly to any such relationship, whereas the narrower term “correlation” refers to a linear relationship between two quantities.
- causal concepts must be traced to some premises that invoke such concepts; it cannot be inferred or derived from statistical associations alone.”
Yule-Simpson’s Paradox

Structural Causal Model
POTENTIAL-OUTCOME FRAMEWORK
The Counterfactual (Potential Outcomes/Neyman-Rubin) Framework
- Causal questions are “what if” questions.
- Extend the logic of randomized experiments to observational data.
Example
假如选择为 ,对应最终结果为 ,那么可以定义 Individual causal effect (ICE) 。
Fundamental Problem of Causal Inference
对于同一个个体而言,我们无法真正同时观察到其做出两种选择之后得到的结果。
- Average causal effect (ACE)
- 对所有人做平均。同时需要注意,这里的“所有人”是包含了 的情况
- 在实际情况下我们能算的平均应该只是
- Standard estimator
- 用于估计 ACE
- 但是需要知道 ACE measures causation measures association
Solve the Problem by Randomized Experiments
如果
那么 ACE 。也就是说 的个体需要 random assignment。
如果 random assignment 无法实现,该怎么办?Ignorability 很难,但是可以考虑 Conditional Ignorability
Propensity score
倾向性得分
这里的 称为混杂因子,可以理解为环境变量。Rubin认为,如果在给定 时, 对 的因果效应消除了混杂因子的影响,那么,在给定一维的倾向性得分 时, 对 的因果效应也是没有混杂因子的影响的,即:
比如在高考完之后,两名同学通过计算倾向性得分,得到上交大的概率都是 ,那么可以认为对这两名同学进行比较是没有 bias 的。
从而 ACE 可以计算为:
Inverse probability weighting
逆概率加权
由于倾向性得分是一维的,那么可以分层,得到平均因果作用的估计。逆概率加权就是连续版本的分层:
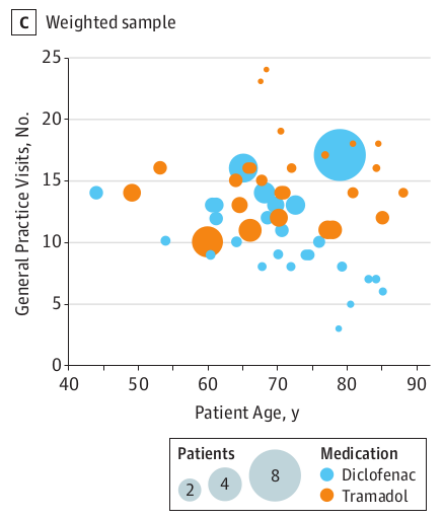
比如对于下图,点的分布本身就与横轴相关。为了消除这个影响,那么就需要除以倾向性得分,使其分布更加趋于均匀。
STRUCTURAL EQUATION MODELS
Weight’s Structural Equation Models
- How can one express mathematically the common understanding that symptoms do not cause diseases?
使用 表示因果不合适,因为方程还可以写成 的对称形式。所以引入 Path Diagram,有

DIRECTED ACYCLIC GRAPH
DAGs Encode Causal Knowledge

Causual assumptions DAG All associations in the system.
- 在 DAG 中,如果两个点之间存在连线,那么说明这两点之间可能存在因果关系
- 如果两个点之间不存在连线,那么说明两点之间一定没有因果关系。
DAGs as SEM
对于 DAG 中的每一个变量 ,如果写成 SEM 的形式,那么有 。在上图中即为:
d-separation
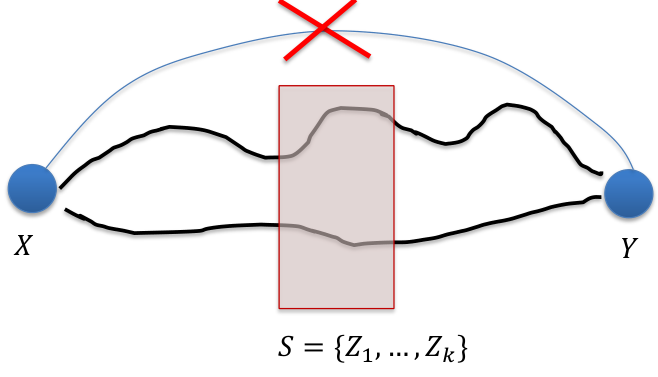
如果一个集合 能够阻断所有 到 的 path,那么称 -separate 和 ,即 。
Discover causal structure by conditional independence
基本思想:
如果能找到 d-separate 和 ,然后固定 中的取值,如果 ,那么说明 之间没有直接因果关系。
PC algorithm
通过条件独立行区分出因果关系来。
- A.) Form the complete undirected graph;
- B.) Remove edges according to n-order conditional independence relations;
- C.) Orient edges by v-structures
- 对于 的结构,当且仅当 不在 中,有
- D.) Orient edges
Step B Example

Markov equivalent class
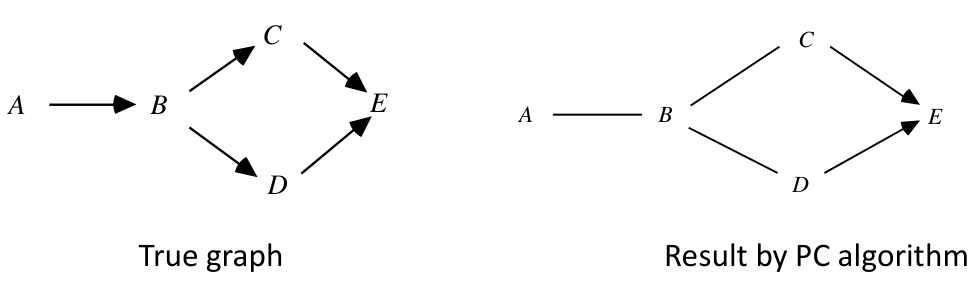
PC 算法无法还原所有的边的方向
这一因为有些因果关系是无法用条件独立性得出的。比如左图的三个结构和右图的两个结构,它们的条件独立性都是相同的。
- Theorem (Verma and Pearl, 1990): two DAGs are Markov equivalent iff they have the same skeleton and the same v-structures.
- skeleton: corresponding undirected graph
- v-structure: substructure with no edge between and
Pearl’s do-calculus
do 操作可以理解为强制的将变量设置为某个值。


A linear non-Gaussian model for causal discovery (LiNGAM)
PC 算法无法处理只有两个变量之间因果关系的问题,因此需要 LiNGAM 方法。
首先考虑 structural equation model,对于两个变量 而言,因果生成关系为
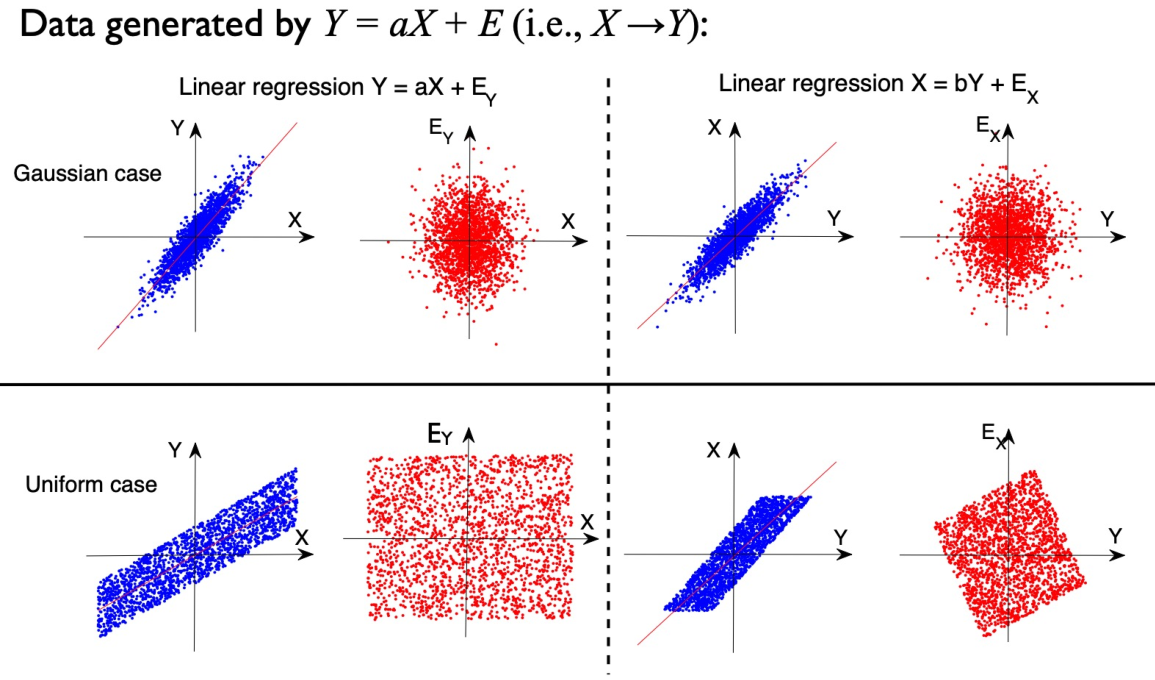
那么此时需要思考当只有 和 的数据时,如何区分 之间的因果关系。因为 同样也可能对应 。现在对 是否为高斯分布进行考虑:
可以发现当 为高斯分布时,因果关系无法区分;但是当 为非高斯分布时(比如图中为均匀分布),那么可以区分,即可以发现此时 与 不独立。
Darmois-Skeitovitch theorem
是由一系列随机变量 线性组合而成
如果 是独立的,那么只要 , 就为高斯分布。此时考虑 的因果关系。
假如我们无法分辨因果关系,那么就说明 是独立的,从而再倒退得到 都是高斯分布。
Linear Non-Gaussian Acyclic Model: LiNGAM
LiNGAM 算法就是利用上述结论建立的算法,用于找到因果关系。那么首先写出 Linear acyclic SEM:
同时需要满足几点基本假设:
- 各个变量的因果关系生成的应当是一张有向无环图
- 外部影响因子(噪音) 应当有 ,同时是相互独立的非高斯随机变量。
- 分析的变量之间没有共同的因(latent confounders)。
接下来对 进行估计:
- 使用 ICA 来估计矩阵
- 生成 DAG
- 除掉那些关联非常弱的边(可能由噪音导致)



Performance of the algorithm
- Fast (ICA is fast)
- Possible local optimum problem (ICA is an iterative method)
- A good estimation needs >1000 sample size for >10 variables
- Not scale invariant